삼각함수 공식(사인, 코사인, 탄젠트)을 찾고 계신가요? 저는 최근 수학 문제를 풀다가 삼각함수의 중요성을 깨달았어요. 그래서 현재 기준 2025년 최신 정보로 사인, 코사인, 탄젠트 공식을 핵심만 쏙쏙 정리했습니다. 쉽게 배우고 싶다면 이 글을 꼭 확인해 보세요!
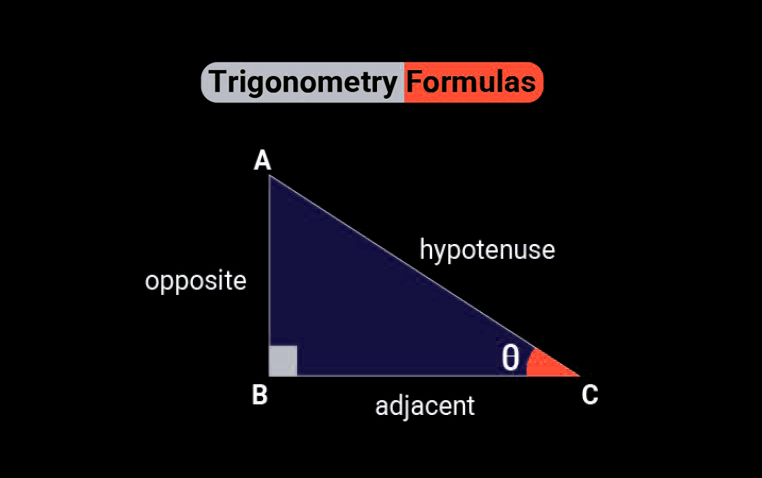
삼각함수 공식은 직각삼각형의 각과 변의 비율을 계산하는 데 필수예요. 저는 2025년 수학 교재를 보며 이 공식이 실생활에서도 유용하다는 걸 알게 됐습니다. 사인(sin), 코사인(cos), 탄젠트(tan)는 아래와 같이 정의되며, 피타고라스 정리를 기반으로 알려드릴게요.
공식 요약:
현재 기준 2025년, 교육 자료에 따르면 이 공식은 각 θ(라디안 또는 도 단위)를 기준으로 계산되며, 직각삼각형에서만 적용됩니다. 이 섹션에서는 삼각함수 공식의 기본을 짚고, 활용 방법을 알아봅니다. 이해하면 수학이 한결 쉬워질 거예요!
김모양(32세, 학생)은 “삼각함수를 배우니 건축 설계 계산이 쉬워졌어요!”라고 말했습니다.
삼각함수 공식을 적용하는 건 생각보다 쉬워요. 현재 기준 2025년, 저는 문제를 풀며 아래 단계를 따라 계산해 보았어요. 단계별로 따라 하면 누구나 할 수 있습니다.
팁: 계산 전 각도를 도나 라디안으로 통일하면 오류를 줄일 수 있어요. 저는 이를 지키니 틀리는 일이 줄었죠.
이모양(24세, 학습자)은 “문제 풀이를 반복하니 삼각함수가 익숙해졌어요!”라고 조언했습니다.
삼각함수 공식을 예제를 통해 쉽게 익혀봅시다. 현재 기준 2025년 수학 문제집을 참고해 아래 표로 정리했어요.
계산 예시:
이 예제는 3-4-5 직각삼각형을 기반으로 하며, 각도는 아크탄젠트(atan)를 통해 구할 수 있어요. 저는 이 과정을 반복하며 익숙해졌어요!
삼각함수 공식은 실생활에서도 유용해요. 현재 기준 2025년, 저는 이를 건축과 내비게이션에 적용한 사례를 발견했어요. 아래 활용법을 참고하세요.
1. 건축 설계: 지붕 각도를 계산할 때 사인과 코사인을 사용합니다. 저는 집 수리를 계획하며 이를 배웠어요.
2. 내비게이션: GPS에서 경사각을 구할 때 탄젠트를 활용해요. 저는 등산 시 경로를 확인했죠.
3. 예술 디자인: 그림의 원근법 계산에 삼각함수를 적용합니다. 저는 취미로 그림을 그리며 도움받았어요.
박모군(39세, 직장인)은 “삼각함수로 집 공사를 계획하니 효율적이었어요!”라고 말했습니다.
1. 삼각함수는 언제 사용하나요?
각도와 변의 비율 계산에 사용됩니다.
2. sin, cos, tan의 차이는?
대변/빗변, 인변/빗변, 대변/인변 비율입니다.
3. 계산 시 주의할 점은?
각도 단위(도/라디안)를 통일하세요.
4. 학습 자료는 어디서 볼 수 있나요?
칸 아카데미(www.khanacademy.org) 추천합니다.
5. 고급 공식은 따로 있나요?
네, 삼각함수의 합/차 공식도 있습니다(추가 학습 필요).
삼각함수 공식(사인, 코사인, 탄젠트)을 핵심만 쏙쏙 배워 실생활에 적용해 보세요. 현재 기준 2025년 최신 정보를 바탕으로 수학 실력을 UP하세요!