대각선 길이 구하는 공식 찾고 계신가요? 피타고라스 정리를 활용하면 쉽게 계산할 수 있습니다. 정사각형과 직사각형의 대각선을 빠르게 구하는 방법을 배워봅시다. 이 글에서 공식과 풀이법을 자세히 알려드리겠습니다.
대각선은 사각형에서 마주보는 두 꼭짓점을 연결하는 직선입니다. 대각선 길이 구하는 공식은 피타고라스 정리를 기반으로 합니다. 직사각형의 경우, 가로와 세로를 이용해 다음과 같이 계산합니다:
대각선 길이 = √(가로² + 세로²)
정사각형의 경우, 가로와 세로가 같으므로 공식이 더 간단해집니다:
정사각형 대각선 길이 = 한 변의 길이 × √2
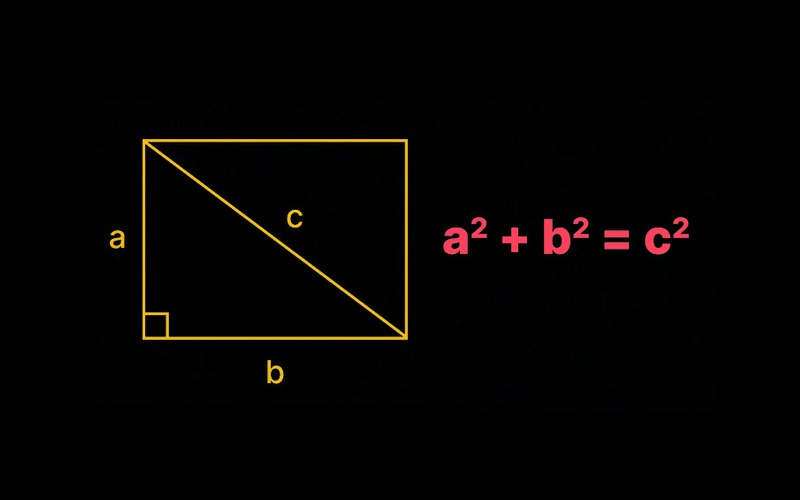
대각선 길이를 계산하는 방법은 간단합니다. 아래 단계별로 따라 해보세요.
대각선 길이 구하는 공식을 예제를 통해 쉽게 이해해 봅시다. 아래 표에서 다양한 사례를 확인하세요.
| 도형 | 가로/한 변 | 세로 | 계산 과정 | 대각선 길이 |
|---|---|---|---|---|
| 직사각형 | 3cm | 4cm | √(3² + 4²) = √(9 + 16) = √25 | 5cm |
| 정사각형 | 5cm | 5cm | 5 × √2 | 약 7.07cm |
| 직사각형 | 6m | 8m | √(6² + 8²) = √(36 + 64) = √100 | 10m |
대각선 길이를 계산할 때 몇 가지 주의사항을 기억하세요.
대각선 길이 구하는 공식은 실생활에서 유용하게 사용됩니다. 아래는 주요 활용 사례입니다.
대각선 길이 공식은 도형에 따라 다릅니다. 아래 표에서 차이점을 확인하세요.
| 도형 | 대각선 공식 | 특징 |
|---|---|---|
| 직사각형 | √(가로² + 세로²) | 가로와 세로 필요 |
| 정사각형 | 한 변 × √2 | 한 변만 알면 계산 가능 |
| 정삼각형 | 한 변 × √3 | 높이 계산 후 적용 |
대각선 길이 구하는 공식을 활용해 쉽게 거리를 계산하세요. 더 많은 수학 정보를 원한다면 아래 링크를 확인해 보세요! 더 자세한 정보는 이곳에서 확인해 보세요!
